Quarta dimensão
Origem: Wikipédia, a enciclopédia livre.
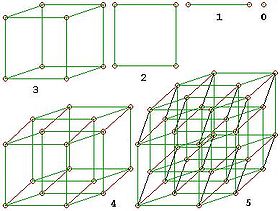
Figura 1. Projeção em 3D de um hipercubo realizando uma rotação simples em torno de um plano que corta a figura de frente para trás e de cima para baixo.
Para ser mais preciso, a quarta dimensão deveria ser identificada com o tempo (ou dimensão temporal). Todavia, entre as décadas de 1870 e 1920 na Grã-Bretanha e nos Estados Unidos, a expressão caiu no gosto popular com o significado de "quarta dimensão espacial" (ou seja, seria na verdade uma "quinta dimensão") e daí disseminou-se por todos os campos das artes e ciências, tornando-se "uma metáfora para o estranho e o misterioso" (Kaku, 2000, p. 41). Portanto, este artigo discute as implicações da quarta dimensão como mais uma dimensão espacial, e não no sentido que lhe é dado, por exemplo, para explicar as teorias sobre o espaço-tempo de Einstein.
A Quarta Dimensão e a Ortogonalidade
Um ângulo reto pode ser definido como um quarto de volta. A geometria cartesiana escolhe arbitrariamente direções ortogonais através do espaço que se constituem em ângulos retos entre si. Três dimensões ortogonais do espaço são conhecidas como comprimento, largura e altura. Portanto, a quarta dimensão é a direção no espaço que está em ângulo reto com estas três dimensões observáveis.[editar] Espaços vetoriais
Um "espaço vetorial" é um conjunto de vetores, que podemos imaginar como flechas presas num determinado lugar do espaço (chamado de origem) e que apontam para outros lugares.Um "ponto" é um objeto com zero dimensão. Não tem extensão no espaço, nem propriedades. Se pensarmos neste ponto como um vetor geométrico, como uma flecha, ele não teria comprimento. Este vetor é chamado de vetor zero e, por si mesmo, constitui-se no vetor espacial mais simples.
Uma "linha" é um objeto unidimensional. Se puxarmos um vetor não-zero em alguma direção, ele terá um comprimento definido. Este vetor tem a "cabeça" em algum ponto no espaço e a "cauda" na origem. Se pensarmos em esticar este vetor duas, três vezes e assim por diante, de modo que ele assuma todos os comprimentos possíveis (mesmo "zero", para obter o vetor zero), teremos uma linha única com uma dimensão de comprimento. Todos os vetores que descrevem pontos nesta linha são ditos como sendo "paralelos" um ao outro. E mesmo que qualquer linha que possamos desenhar tenha alguma espessura mínima (para que possamos vê-la), esta linha idealizada não a possui.(...)
LEIA MAIS EM : http://pt.wikipedia.org/wiki/Quarta_dimens%C3%A3o


ESTA DIMENSÃO SERVE COMO UM PORTAL...E A IMAGEM LINDA...RSRS...DANÇANDO EM TORNO DELE...BEIJOS...AZUIS...
ResponderExcluir